AI is like fire.
We have had radical technological advancements in recent history. Social media, augmented reality, platform shifts like web, mobile. But AI is way more significant of a technology. It is as significant as the discovery of fire. It has the potential to change the trajectory of the evolution of our species.
One of the holy grails of unlocking this potential of AI is to build systems that can reason like humans. By improving AI's, Large Language Models in particular, ability to break down complex problems and apply logical steps.
Bagel's research team has been exploring this problem. Analyzing LLM building techniques, especially fine-tuning techniques, to allow Large Language Models to evolve from pattern-recognizing prediction agents to true cognitive agents. Our deep research spanned three major types of reasoning, aka intelligence: arithmetic, commonsense, and symbolic.
Today, we're sharing our findings. This research targets the core of what we believe to be the ultimate AI evolution, human-level reasoning. Or beyond (God level?).
We have explored techniques for the training and fine-tuning phases of model development. We have also ventured into the absolutely fascinating world of inference-time reasoning. This is where LLMs can be built or fine-tuned to generate novel solutions during inference, even if the solutions aren't part of their training dataset.
Dive in. And if you're in a rush, we have a TLDR at the end.
Types of Reasoning
Varied types of reasoning tasks stretch AI's abilities. First, let's understand how they're defined.
Arithmetic reasoning pushes machine learning to test problem-solving in a clear way. It forces models to break down problems. Choose from many strategies. Connect steps to find solutions. This makes math different. It shows exactly how well models can grasp details. And use the right solution steps in order.
Commonsense reasoning upends our expectations. Models must understand the strange logic of everyday life. The challenges emerge when systems face the quirks of human interactions. The implicit rules we take for granted. For example, a door opens before you walk through. Time flows forward not backward. Water makes things wet. These obvious truths become complex puzzles for artificial systems to unravel.
Symbolic reasoning flips the script on traditional machine learning. While neural networks excel at fuzzy pattern matching, symbols demand precision. Models must follow strict rules. Manipulate abstract concepts. Chain logical steps. Like a careful mathematician rather than an intuitive artist. The symbols hold no inherent meaning. Yet through them, we build towers of logic that reach toward human-level reasoning.
Beyond these core types, reasoning takes many forms. Logical deduction draws rigid conclusions while induction makes creative leaps. Causal reasoning traces the hidden threads between actions and consequences. Multimodal reasoning juggles text, images, and data in a complex combination of understanding. Knowledge graphs map the relationship of facts and relationships. Yet all serve one goal - moving AI from pattern matching toward true comprehension. From memorized responses to novel insights. From prediction to understanding.
Below, we look into training time and inference time approaches to enhance these types of reasoning.
1. Training Time Approaches
1.1. Fine-Tuning Approaches
Parameter Efficient Fine-Tuning (PEFT)
How it works: PEFT reverses traditional model adaptation (Hu et al. 2023). Four methods reveal new techniques.
Prompt-based learning embeds adjustable signals into frozen models. Prefix-tuning and P-tuning introduce small changes. These changes alter outputs without altering the main model.
Reparametrization methods like LoRA simplify complex weight matrices. They turn large updates into efficient low-rank forms. LoRA captures patterns from high-dimensional spaces with minimal adjustment.
Adapters create extra neural pathways. Series adapters stack, each layer adjusting outputs gradually. Parallel adapters develop side skills, keeping the base intact.
Adapter placement is key. Series adapters fit after MLP layers. Parallel adapters excel within them. LoRA touches both attention and MLP layers. Each method targets the right spot.
Why it's useful: PEFT reduces resource demands. Large models gain new abilities without major changes. PEFT preserves the base while adding specialized skills. Hardware that struggled with fine-tuning now handles complex updates.
Tradeoffs: Not all tasks fit PEFT. Some models need deeper changes. Base model limitations still exist. Combining methods is tricky. PEFT may struggle with very complex tasks.
WizardMath
How it works: WizardMath learns in three distinct steps (Luo et al., 2023).
First is supervised fine-tuning. Here, the model picks up raw mathematical patterns. It starts recognizing basic structures. Patterns get mapped to solutions. This step builds intuition for common operations. The foundation is set.
Next, instruction reward models refine the process. They judge both answers and methods. These models look for efficiency. They guide the model toward elegant solutions. The focus shifts from correctness to quality.
Finally, PPO-based reinforcement learning enhances problem-solving. The model tests ideas, adapts, and improves. Evol-Instruct feedback loops refine its logic with each run (Xu et al. 2023). It gets better at selecting strategies.

Why it's Useful: Most models just match patterns. WizardMath thinks in logical steps. It breaks down problems like a mathematician. It selects methods based on understanding, not memory. This leads to solutions that are both effective and precise.
Tradeoffs: Training WizardMath takes heavy computational resources. Its deep math focus limits general use. Low-quality data can introduce errors. Practical solutions can sometimes lose to elegant ones.
Divergent Chain of Thought (DCoT)
How it works: DCoT breaks the single-path approach (Puerto et al. 2024). Multiple paths form at once. Each one tackles the problem differently. Yet all conclude in a single inference.
Zero-shot generation creates diverse solutions. Every path seeks the truth. Each follows its own course. Some are direct. Others are more complex. All valid. The model acts like a group of experts. Each path offers a different view.
These paths then interact. Strong strategies merge. Weak points become clear. The model learns to assess its own reasoning. It compares methods. It blends insights. All this happens without extra training.
Why it's Useful: Multiple paths offer built-in validation. When paths align, certainty rises. When they don’t, issues appear. Different views reveal hidden details. Diversity deepens understanding.
Tradeoffs: More paths need more computation. Balancing variety and consistency is tricky. Conflicting paths need resolving. For simple tasks, it's overkill. A group isn't always better than one.
1.2. Pre-training and Knowledge Transfer
Continued Pre-training
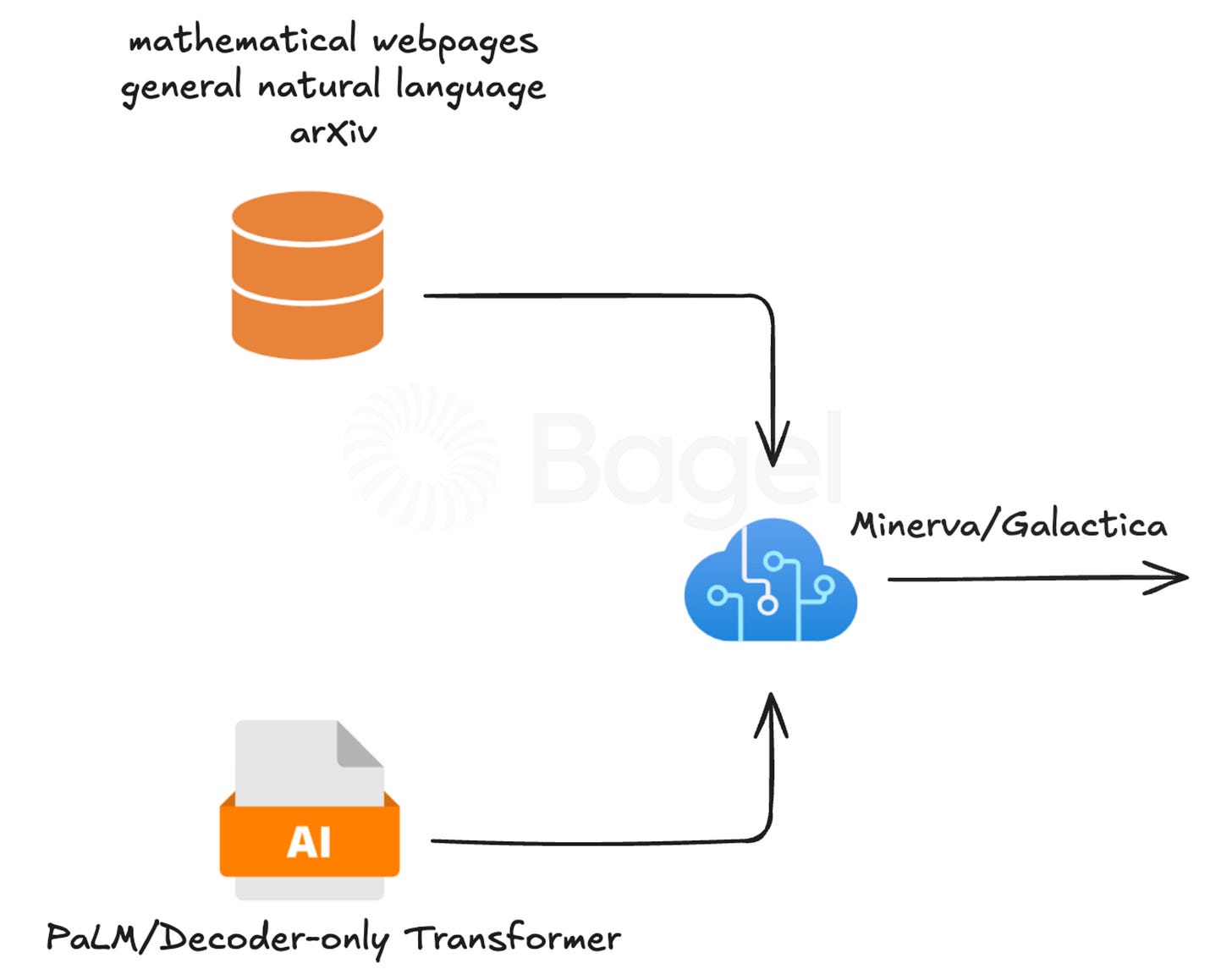
How it works: Models like Galactica (Taylor et al. 2022) and MINERVA (Lewkowycz et al. 2022) go beyond standard training. They learn from over 100 billion tokens of scientific data. This includes mathematical papers, scientific articles, and technical documentation. Raw data is converted into structured knowledge.
Galactica includes tokens for specific scientific terms. It treats citations as part of the vocabulary. Chemical formulas become meaningful. Mathematical symbols are treated like tools. It learns the language of science.
MINERVA focuses on quantitative reasoning. It answers natural language questions in physics, chemistry, and economics. Converts questions into math formulas. Uses LaTeX to present detailed solutions. It performs the calculations on its own.
Why it's useful: Smaller models can surpass larger ones in specific fields. They grasp complex math. Work with technical notation naturally. The gap between general models and experts shrinks.
Tradeoffs: Training costs rise. Each field requires massive new data. As new knowledge grows, old knowledge fades. Balancing focus and breadth is hard. It might be great at physics but weak in other areas.
Curriculum Learning
How it Works: Learning transforms from random sampling to structured progression (Adyasha & Maharana 2022). Like evolution, but guided. Deliberate. Purposeful.
A teacher network ranks training samples. Easy concepts come first. Complex ideas build on simple ones. The pacing function controls the flow of knowledge. Sometimes fixed. Sometimes adaptive. Responds to the model's growing understanding.
Three methods measure sample difficulty. Question Answering Probability tracks how often the model succeeds. Model Variability watches for consistent responses. Energy-based scoring identifies outliers and edge cases. The curriculum adapts based on these signals.
Why it's Useful: Models learn more efficiently. They build strong foundations before tackling complexity. Understanding grows naturally. Organically. Each concept reinforces the last. Difficult ideas become manageable when approached in sequence.
Tradeoffs: Designing effective curricula challenges even experts. Learning time stretches longer. Some concepts resist ordered progression. The path from simple to complex isn't always clear. Sometimes chaos teaches better than order.
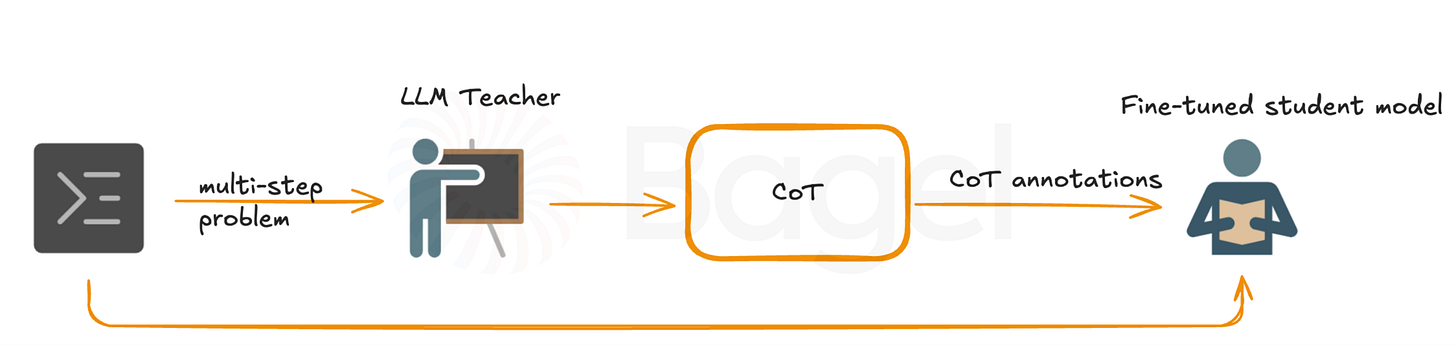
CoT Knowledge Distillation
How it Works: Large models become teachers. Small models become students. Knowledge transfers through carefully curated examples (Magister et al. 2023).
The process splits into two phases. First, generate Chain of Thought data. Large models solve problems step by step. Show their work. Create a roadmap of reasoning. Only correct solutions make the cut. Quality matters more than quantity.
Then comes student fine-tuning. Small models learn from these examples. They see not just answers but thinking processes. The target answer guides early steps. This prevents small errors from derailing entire solutions. Teacher forcing ensures the student stays on track.
Why it's Useful: Advanced reasoning becomes accessible to smaller models. Complex problem-solving skills transfer efficiently. Small models learn to think clearly with limited resources. They gain the wisdom of larger models without the computational burden.
Tradeoffs: Some sophistication gets lost in translation. Students never quite match their teachers. The distillation process demands careful curation. Bad examples can teach bad habits. The balance between compression and comprehension remains delicate.
2. Inference Time Approaches
2.1. Chain-Based Methods
Chain of Thought (CoT)
How it works: Wei et al. redefined reasoning with their 2022 paper. They introduced language models to step-by-step problem-solving using just eight examples. These guided models unlock hidden potential.
With precise prompts, models show their internal reasoning. No need for new training or changes to the model. This latent capability is accessed by using strategic examples.
The models learn to break down problems into logical steps that mimic human thinking. Each step becomes clear. The internal thought process shifts from a black box to a visible sequence.
This approach scaled well. PaLM, with chain-of-thought prompting, hit 75.6% on StrategyQA. Even sports questions saw 95.4% accuracy, surpassing human experts. Complex math problems were solved with clear, step-by-step reasoning. In commonsense tasks, hidden assumptions surfaced in natural language. Symbolic problems became easy to follow.
Why it's useful: Wei et al.'s work showed breakthroughs across fields. LaMDA 137B demonstrated this by generating 96% correct answers with sound reasoning. Problem-solving became transparent. Larger models produced more coherent explanations.
Tradeoffs: Reasoning sometimes fails. Models can get confused. Wei’s research showed that 46% of wrong answers had minor mistakes, while 54% had major logical errors. Sequential reasoning can hit barriers. Complex tasks push models to their limits.
Program of Thought (PoT)
How it works: Chen et al.'s 2022 work changed how models approach math. They turned natural language into executable programs that solve complex problems with machine-level precision.
The process is seamless. Word problems convert directly into Python code. Variables capture key details from the text. Functions embody solution strategies. Algorithms emerge from simple descriptions. The model coordinates external tools with precision.
PoT set new records, improving math benchmarks by 8% in few-shot settings. In zero-shot, the gains were 12%. The code tells a story with structured logic. Control flows mirror human thought. Programs serve as both solution and explanation.
PAL expanded on this. Gao et al. in 2023 showed how models could use Python interpreters for better reasoning. Complex calculations became sharper. Formal math operations translated into natural expression.
Why it's useful: Precision dominates. Math problems flow into code. The model combines high-level reasoning with computational accuracy. It's like a mathematician working alongside a supercomputer.
Tradeoffs: Some problems don't translate well into code. Executing programs raises security concerns. The model must handle both natural language and code, increasing the risk of errors.
2.2. Consistency and Verification Methods
Self-Consistency (SC)
How it works: Wang et al. introduced SC in 2022, shifting from greedy decoding to statistical sampling. This method changes inference entirely.
Instead of one solution, each step produces multiple paths. SC explores various reasoning attempts at once. The decoder samples different trajectories in the probability space. Errors are reduced by repeating steps, leading to validation through sampling.
SC’s statistical foundation is strong. It marginalizes over samples to minimize errors in individual paths. Think of it like quantum mechanics: multiple paths exist, and truth emerges from the statistical patterns.
Their approach was groundbreaking. The decoder generates n unique reasoning chains, each following a different probability path. Final answers come from majority voting, but the process goes beyond simple counts.
Wang's team tested models from UL2-20B to PaLM-540B. Accuracy increased across the board. Smaller models showed the most improvement, indicating SC unlocks hidden potential in models of all sizes.
Why it's useful: Numbers tell the story. Multiple paths automatically validate answers. Different paths catch edge cases. Robustness increases as more paths are explored. Quantity becomes quality.
Tradeoffs: Computation grows costly. Each path demands resources. Memory use spikes. Contradictory paths sometimes arise. Resolving these conflicts adds complexity.
Self-Endorsement (SE)
How it works: Wang et al.’s 2024 paper introduced SE, a new verification method. The system generates diverse responses and then analyzes them. Facts are extracted, labeled, and compared. Cross-response validation assigns endorsement scores to each fact.
SE uses advanced fact extraction algorithms. Neural retrieval identifies key claims, and automatic cross-referencing helps the model distinguish strong facts from weaker ones. This statistical validation process drives the system.
High-scoring facts shape future outputs, while low-scoring ones lead to re-evaluation. Each pass refines the model’s response through consistency.
The fact extraction pipeline is highly technical. Named entity recognition identifies key elements, and relation extraction maps connections. All of this occurs without human input.
Why it's useful: Accuracy improves. Hallucinations drop. The system validates its own facts. Confidence scores make responses more reliable.
Tradeoffs: Processing takes longer. Fact extraction sometimes fails. Complex statements resist simple validation. Some valid facts get rejected if they don’t fit the statistical pattern.
Least-to-Most Prompting (LM)
How it works: Zhou et al. introduced LM in 2022, a system that breaks tasks into smaller parts and solves them step by step.
The process follows phases. First, the model analyzes the input. Next, it identifies sub-tasks. Then, it solves each part. Finally, it combines the results. Each phase builds on the previous one.
For example, in the last-letter task with "cat dog bird," the model processes each word separately. It finds ‘t’ from "cat," ‘g’ from "dog," and ‘d’ from "bird." Then, it combines them into "tgd." The model achieved 94% accuracy with four words and 74% even with twelve.
Errors are predictable. Sometimes letters drop during connection. Sometimes extras appear. But it rarely confuses the final letter of each word.
Why it's useful: LM is highly efficient. It only needs two examples to work well. It uses less tokens than traditional methods, achieving equal or better results.
Scaling is impressive. The model handles sequences four times longer than its training examples without losing accuracy. Standard methods fail on long sequences, scoring 31.8% on twelve-word tests. LM hits 74%, with a growing advantage on harder tasks.
Tradeoffs: Some tasks don't split easily. Certain problems need a different approach. The method requires more steps, which adds processing time.
Technical limits arise. The model must track partial solutions, and memory usage grows with longer sequences. Some tasks need several attempts to find the best split.
Careful planning is essential. The order of sub-tasks affects accuracy, and managing information efficiently becomes critical. The system must adapt its splitting strategy for different problems.
How to Test for Reasoning
Cognitive sciences have studied human reasoning since experimental psychology emerged in the late 19th century. This field has been crucial for technological development, education improvement, cognitive disorder treatment, and better decision-making. Scientists use various tools to study reasoning, including problem-solving tasks, computational models, brain imaging (fMRI and EEG), and behavioral measurements like eye-tracking. These combined methods help researchers understand how humans reason.
Analogously, AI researchers have invented reasoning tasks to test the reasoning capabilities of LLMs in the form of special datasets. Being AI more of an engineering field and computer science field, these datasets provide a rigorous benchmark to test AI systems. This allows researchers to measure a model’s accuracy and identify areas where it may be falling short.
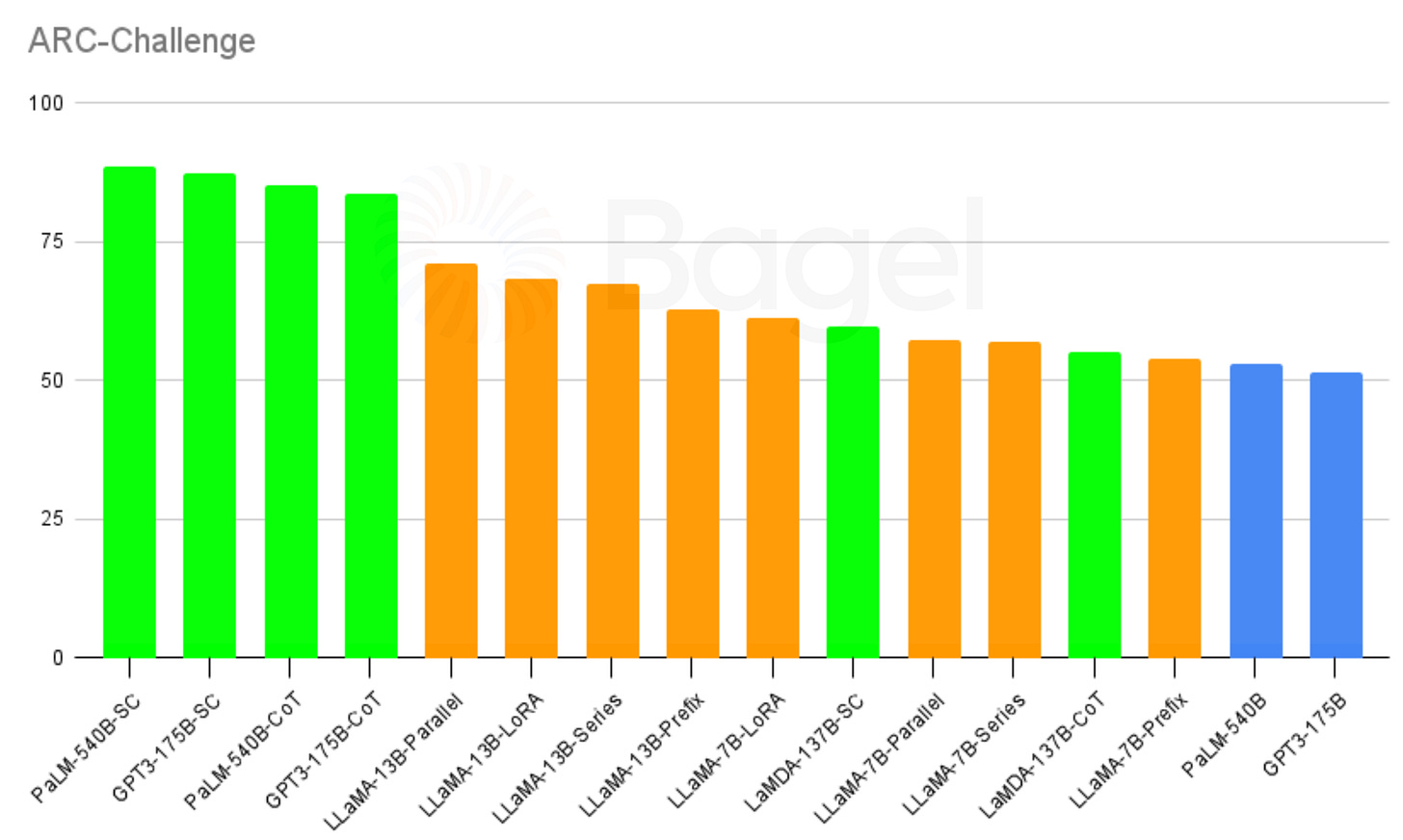
Datasets for testing AI reasoning on one type of reasoning should be diverse around that type of reasoning in order to test various complexities and nuances in tasks. For example, to evaluate language models' common sense capabilities, a dataset like ARC is used. The figure below we shows a ranking of the best LLMs for the ARC-challenge dataset taken from different sources.
Inference-time techniques appear in green, training-time techniques appear in orange, and standard base models appear in blue.
In the image above, the best performing techniques correspond to inference-time approaches, in particular, SC has a clear advantage over standard CoT. The fine-tuning approaches cannot match the inference-time approaches where they show a clear advantage.
TLDR
Our research focuses on strengthening reasoning in Large Language Models (LLMs) in three ways. First, arithmetic reasoning - approaching math problems logically. Next, commonsense reasoning - grasping everyday situations and drawing conclusions. Finally, symbolic reasoning - handling abstract symbols by strict logic.
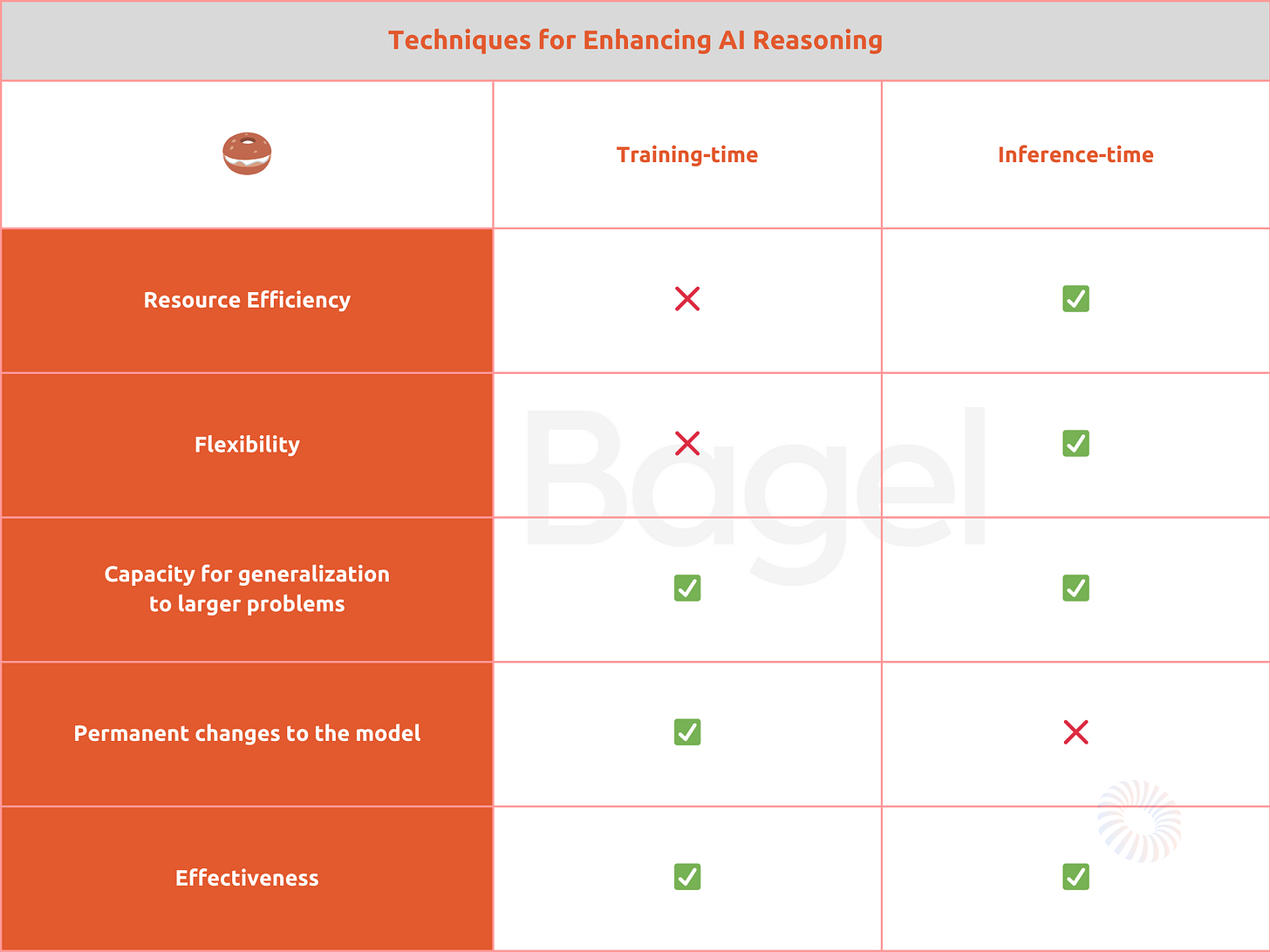
We explore two strategies to push these areas forward. First are training-time methods. These adjust AI’s learning process, adjusting it for specific tasks but needing time and computing power. For example, WizardMath teaches detailed problem-solving for math, while PEFT (Parameter Efficient Fine-Tuning) builds skills without huge resources. DCoT (Divergent Chain of Thought) allows AI to consider multiple solutions simultaneously.
The second approach is Inference-time methods. These enhance existing models without retraining, bringing quick improvements, though sometimes with less depth. Chain of Thought (CoT) prompts AI to explain each step it takes. Program of Thought (PoT) has AI write and run code to boost accuracy. Self-Consistency (SC) checks multiple paths to ensure reliable answers.
The below table is a summary of our findings.
By open-sourcing our research on AI reasoning, our team at Bagel aims to collaborate with the Open Source AI community to forge humanity's next chapter.
Bagel, Monetizable Open Source AI.